Medium - Understanding Neural Networks
in Trend
Trend 파악을 위한 Medium 기고문 포스팅 - 뉴럴 네트워크에 대한 이해; 뉴럴 네트워크가 어떻게 동작하는지 알아보면서 딥러닝에 대해 알아봅시다.

딥러닝은 요즘 아주 핫한 주제입니다. 그렇지만 무엇이 다른 머신러닝에 비해서 그렇게 특별한 것일까요? 이것은 꽤나 심도있는 질문이기 때문에 먼저 뉴럴 네트워크의 기본에 대해 배워봅시다. 인공신경망 네트워크는 딥러닝의 작업의 핵심입니다. 블랙박스 처럼 보이지만 실제로 깊게 파고 들어가보면 다른 모델처럼 예측을 달성하기 위한 것이죠. 이 포스트에서는 인공신경망 네트워크에 대해서 알아보고 결과적으로 어떻게 동작하는지, 뭘 하는건지 직관적으로 이해할 수 있게 되면 좋겠습니다.
The 30,000 Feet View
먼저 우리가 다룰 수 있는 최상위 레벨에서 시작합니다. ** 신경 네트워크는 다수의 뉴런 네트워크로 우리가 예측을 하는데 사용하는 것입니다. ** 아래의 다어이그램은 5개의 입력을 받고 5개의 출력을 내뱉는 2개의 히든 레이어를 가진 신경 네트워크 입니다.

Neural network with two hidden layers
먼저 왼쪽에서 부터 설명을 드리겠습니다.
- 우리 모델의 입력값은 오랜지 색입니다.
- 뉴런의 첫번째 히든 레이어는 파란색입니다.
- 뉴런의 두번째 히든 레이어는 자주색입니다.
- 우리 모델의 출력 결과는 초록색입니다.
점들을 잇는 선은 모든 뉴런이 어떻게 내부적으로 연결되어 있고 입력 레이어로부터 출력 레이어까지 어떤 경로를 거치는지 보여줍니다. 나중에 우리는 각 결과값에 대해서 단계별로 계산을 해볼 것입니다. 또한 신경 네트워크에서 회고로 알려진 실수에서 배우는 것을 어떻게 하는지 알아볼 것입니다.
Getting our Bearings
먼저 우리의 방향성부터 확실히 합시다. 신경 네트워크는 정확히 뭘 하려는 것일까요? 다른 모델처럼 정확한 예측을 하려고 하는 것입니다. 입력값들과 짝을 이루는 결과 값들이 주어진다면 우리는 이러한 데이터 셋을 이용해서 입력값을 받으면 최대한 비슷한 결과값을 뱉어주려고 하는 것입니다.
위에서 그렸던 복잡한 그림은 잊어버리시고 지금은 아래의 간단한 신경 네트워크를 봅시다.

Logistic regression (with only one feature) implemented via a neural network
이것은 신경 네트워크로 단일 회고 논리를 표현한 것입니다. 회고 논리 방정식을 다시 정의하고 싶다면 위의 그림에서 보였던 네트워크 요소와 방정식 요소의 색깔을 비교하시면 됩니다.
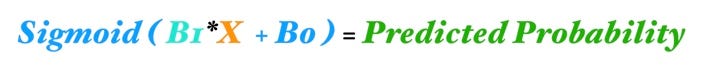
Logistic regression equation
각 요소를 알아봅시다.
- X (오렌지색) 는 우리의 단일 입력값으로 모델의 예측을 위해 주어집니다.
- B1 (청록색)은 우리의 단일 회고 논리에서 예측에 사용될 매개변수 입니다. B1은 입력값 X와 히든 레이어 1에 있는 파란색 뉴런과 연결하는 선이라는 것이 중요합니다.
- B0는 바이어스로 리그레션에서 인터셉트 텀과 매우 유사합니다. 신경 네트워크에서의 차이점은 모든 뉴런은 자신의 바이어스가 있다는 것이죠. 리그레션에서 모델은 오직 하나의 인터셉트 텀을 가집니다.
- 파란색 뉴런은 sigmoid 활성 함수를 포함하고 있습니다 ( 파란색 내부의 곡선을 가리킵니다. ) sigmoid 함수는 log-odds에서 probability로 가는데 사용됩니다.
- 그리고
(B1*X+B0)의 값에 sigmoid함수를 적용하면 예측 값을 얻게됩니다.
그리 나쁘진 않죠? 좀 더 개량해봅시다. 초간단 신경 네트워크는 다음과 같은 컴포넌트들로 구성됩니다.
- 연결 ( 예제에는 여러개의 커넥션이 있으며 각각에는 뉴런으로 연결될 때 가중치가 있습니다. ) 내부에는 가중치가 있으며 B1(입력) 을 변환하여 뉴런으로 전달합니다.
- 뉴런은 B0 바이어스를 가지고 있으며 활성 함수인 sigmoid를 가지고 있습니다.
** 그리고 이 두 객체들이 뉴런 네트워크를 구성하는 기본 요소입니다 ** 더욱 복잡한 신경 네트워크들이 많지만 단지 히든 레이어들이 더 많거나 (뉴런이 많음) 뉴런 사이의 연결이 많은 정도 입니다. 그리고 연결망이 더욱 복잡해지는 것이 우리가 뉴런 네트워크가 학습한다고 일컫는 것이며 우리의 입력-결과 값과 히든 레이어들 간의 연결을 말하는 것입니다.
Let’s Add a Bit of Complexity Now
이제 기본 프레임워크는 알게 되었으니 다시 살짝 복잡한 뉴런 네트워크로 돌아갑시다. 그리고 입력에서 결과값으로 가는 것을 살펴봅시다.

Our slightly more complicated neural network
첫번째 히든 레이어는 두개의 뉴런으로 구성되어 있습니다. 그래서 5개의 입력들은 첫번째 히든레이어의 뉴런에게 연결되어야 하고 총 10개의 연결이 생깁니다. 다음 이미지는 입력1과 히든 레이어1과의 연결을 보여줍니다.

The connections between Input 1 and Hidden Layer 1
주목하셔야 할점은 연결에 가중치가 있다는 것입니다. W1,1은 입력 1과 뉴런 1 사이의 연결을 의미하며 W1,2는 입력 1과 뉴런2의 입력을 말합니다. 따라서 Wa,b는 입력 a에서 뉴런 b사이의 연결이 됩니다. 이제 히든 레이어에 있는 각 뉴런들의 결과를 계산합시다. 여기에서는 다음과 같은 공식을 사용할 것입니다.
Z1 = W1*In1 + W2*In2 + W3*In3 + W4*In4 + W5*In5 + Bias_Neuron1
Neuron 1 Activation = Sigmoid(Z1)
이러한 계산을 하기 위해 다음과 같이 행렬을 쓸 것입니다.

Matrix math makes our life easier
이전 계층이 m개의 요소이고 현재 계층이 n개의 요소일 때 뉴럴네트워크는 다음과 같이 일반화 할 수 있습니다.
[W] @ [X] + [Bias] = [Z] [W]는 가중치를 나타내는 NxM 행렬이고 [X]는 Mx1 행렬로 입력이나 이전 레이어의 액티베이션에서 가져오는 것이며 [Bias]는 Nx1 행렬로 뉴런 바이어스며 [Z]는 Nx1 행렬로 중간 결과값입니다. 위의 공식에서는 파이썬 표기법을 따라서 행렬 곱셈에 앳(@)표시를 사용했습니다. 우리가 [Z]를 얻어내면 각 요소를 활성화 함수에 적용할 수 있으며 현재 레이어의 결과값을 얻어낼 수 있습니다.
마지막으로 우리가 다음으로 가기전에 이런 요소들을 시각화 하겠습니다.

Visualizing [W], [X], and [Z]
반복적으로 [Z]를 계산하고 활성 함수에 적용을 함으로써 우리는 입력에서 결과값으로 갈 수 있습니다. 이런 프로세스가 전방 전파입니다. 이제 결과값이 어떻게 계산되는지 알았으니 결과값을 평가하는 법과 뉴럴 네트워크를 학습하는 법에 대해서 알아봅시다.
Time for the Neural Network to Learn
포스팅 내용이 길어질거 같으니 커피 한잔이라도 드시고 오세요. 준비가 되셨나요? 이제 우리는 뉴런 네트워크의 결과가 어떻게 계산되는지 알았으니 학습에 대해서 알아볼 것입니다. 상위수준에서 바라본 뉴런 네트워크의 학습은 다른 데이터 과학 모델과 비슷합니다. cost 함수를 정의하고 최소화하기 위해 gradient descent optimization을 사용합니다.
먼저 cost function을 최소화하기 위해서 우리가 당길 수 있는 레버가 무엇인지 생각해 봅시다. traditional linear, logistic regression 에서는 beta 계수 ( B0, B1, B2 등)를 찾아서 cost function을 최소화합니다. 신경 네트워크에서는 같은 일을 하지만 더욱 복잡하고 큰 규모로 수행합니다.
traditional regression에서 우리는 특정 beta를 독립시켜서 값을 변화시켜도 다른 계수에게 영향을 주지않게 할 수 있습니다. 따라서 각 beta 계수를 독립시키고 cost function에 주는 영향을 확인하면서 어떻게 해야 cost function을 최소화할 수 있는지 알아내는 것이죠.

Five feature logistic regression implemented via a neural network
신경 네트워크에서는 한 연결의 가중치를 바꾸게 되면 해당 뉴런 하위 계층에 모두 전달되게 됩니다. 따라서 각 뉴런은 작은 하나의 신경네트워크 처럼 동작하게 됩니다. 예를들어 우리가 logistic regression 5개를 원하는 경우 위의 그림처럼 뉴런과 5개의 연결로 표현할 수 있습니다.
따라서 각 히든 레이의 신경 네트워크들은 결과물을 하위 계층에게 공급하는 모델 스택들이라고 할 수 있습니다.
The Cost Function
이렇게 복잡도가 높다면 우리가 뭘 할 수 있을까요? 너무 낙심하지 마시고 차근차근 단계를 밟아봅시다. 먼저 우리의 목적을 확실하게 해봅시다. 학습 데이터가 주어지면 그것을 사용해 결과물을 뱉는 것입니다. 우리가 찾고자 하는 것은 가중치의 집합들이며 cost function을 최소화할 수 있는 상수들입니다. cost function은 우리의 예측이 실제 결과와 얼마나 연관성이 있는지 평가하는 것입니다.
신경 네트워크를 학습시키기 위해서 우리는 Mean Squared Error(MSE)를 cost function으로 사용할 것입니다.
MSE = Sum [(Prediction - Actual)^2]*(1/num_observations)
MSE 모델은 평균적인 오류를 알려주지만 예측의 오류값을 평균내기 전에 제곱을 하므로 오차가 좀 있습니다. 값을 아주 조금만 바꿔도 엄청나게 영향이 가는 것이죠. linear regression 의 cost function 과 logistic regression 또한 비슷하게 동작합니다.
좋습니다 그러면 우리가 해야할 일은 cost function을 최소화 하는 것이죠. gradient descent를 사용해야할 때인거 같죠? 하지만 아직은 아닙니다. gradient descent를 사용하려면 cost function의 gradient를 알아야하고 가장 급격한 방향을 가리키는 벡터도 알아야합니다. 뉴럴 네트워크에서는 바꿀 수 있는 가중치들이 매우 매우 많으며 서로 연결되어 있습니다. 이런 gradient 들을 어떻게 계산해야할까요? 다음 섹션에서는 backpropagation을 이용해서 이 문제를 어떻게 해결하는지 보여드리겠습니다.
Quick Review of Gradient Descent
함수의 기울기는 각 매개변수들이 어디로 향하는지 알려주는 벡터입니다. 예를들어 우리가 cost function을 최소화 하려고 하고 C(B0, B1) 두개의 매개변수가 있을 때 기울기는 다음과 같습니다.
Gradient of C(B0, B1) = [ [dC/dB0], [dC/dB1] ]
따라서 각 요소들의 기울기는 우리가 특정 매개변수를 변경했을 때 cost function이 어떻게 바뀔지 알려줍니다. 그래서 우리는 어떤걸 얼마나 비틀지 알아내려고 하는 것이죠. 요약하자면 최소화를 하기위해서는 다음과 같은 단계가 필요합니다.

Illustration of Gradient Descent
- 현재 위치에 대한 기울기를 계산합니다.
- 각 매개변수에 대해서 기울기의 방향과 반대방향으로 요동치게 만듭니다.
- 변경된 매개변수에 대해 새롭게 기울기를 계산하고 최소값이 될 때까지 이전 단계를 반복합니다.
Backpropagation
이쯤에서 무료 온라인 텍스트 북을 언급하려고 합니다 뉴럴 네트워크에 대해서 더욱 깊게 이해하고 싶다면 꼭 확인하세요. 물론 우리는 backpropagation이 어떻게 왜 동작하는지 직관적으로 이해하기 위한 것을 만들어 볼 것입니다.
forward propagation은 뉴럴 네트워크에서 앞으로 전진하는 것이라는 것을 기억하세요 ( 입력을 통해 예측을 하는 것입니다. ) backpropagation은 반대입니다. signal이 아니라 에러를 모델의 뒤로 보내는 것입니다. 간단한 시각화 자료들이 backpropagation을 이해할 때 저에게 큰 도움이 되었습니다. 아래의 그림은 입력에서 결과로 나아가는 forward propagation 입니다. 이 프로세스는 다음과 같은 절차로 요약할 수 있습니다.
파랑색 계층의 뉴런에게 주어지는 입력값은 가중치, 상수이며 각 뉴런에 sigmoid 함수를 적용하여 활성값을 얻습니다. 예를들면 이런 것이죠 Activation_1 = Sigmoid( Bias_1 + W1*Input_1 )
파랑색 계층의 결과값인 활성값1과 활성값2는 자주색 뉴런에게 입력값으로 주어지며 최종적인 결과 값을 산출합니다. 따라서 전방전파의 목적은 각 뉴런의 활성값을 계산해서 결과값으로 나아가는 것입니다.

Forward propagation in a neural network
이제 이것을 뒤집어 봅시다. 아래의 그림에서 빨간색 화살표를 따라가면 자주색 뉴런에서 시작한다는 것을 알게되셨을 겁니다. 우리의 결과 활성값은 예측에도 사용되고 모델 오류 수정을 위한 입력값이 됩니다. 이런 에러를 전방전파에 쓰였던 것과 동일한 가중치와 연결로 후방전파합니다.
전방전파의 목적이 우리가 결과를 얻을 때까지 계층을 거치며 계산을 하는 것이라는 것을 기억한다면 후방전파의 목적도 비슷하게 정의할 수 있을 것입니다.
우리는 우리의 모델에게 전달되는 오류값을 통해 각 뉴런들의 오차를 계산하려고 합니다.

Backpropagation in a neural network
그렇다면 왜 각 뉴런의 오차들을 신경써야할까요? 신경 네트워크의 두 구성요소는 연결과 특정 뉴런으로 신호를 전달하는 것입니다. 이러한 가중치와 상수 값들은 네트워크 전체에 전달되며 모델의 예측값에 영향을 미치게 됩니다 이 부분은 매우 중요합니다. 특정 뉴런의 오차는 모든 뉴런과 연결되어 있기때문에 직접적으로 우리의 cost function에 영향을 주게 됩니다.
따라서 각 뉴런의 오차들은 입력값을 대신하는 cost function의 일부입니다. 때문에 직관적으로 생각해본다면 특정 뉴런이 다른 것들보다 훨씬 큰 오차를 가지고 있다면 가중치와 상수값을 바꾼다면 다른 뉴런들보다 더욱 더 크게 결과값에 영향을 줄 것입니다. 따라서 근본적으로 후방전파는 우리가 각 뉴런의 오차값들을 계산할 수 있게해줘서 기울기를 줄일 수 있도록 해주는 것입니다.
An Analogy that Helps - The Blame Game
정말 방대한 양이었기 때문에 이 분석이 도움이 되었으면 좋겠습니다. 대개의 사람들은 직장에 끔찍한 동료들을 갖고 있을 거입니다. 항상 남을 비난하고 잘못된 방향으로 일이 흘러가게 문제를 만드는 사람들이죠. 뉴런들은 후방전파를 통해 blame game의 전문가가 됩니다. 에러가 특정 뉴런에게 전파되면 그 뉴런은 아주 신속하고 정확하게 이 에러가 어디로부터 왔는지 가리킵니다.
그럼 각 뉴런들은 다른 뉴런들을 관찰하지 않고 어떻게 누가 잘못되는지 아는 것일까요? 뉴런들은 그냥 가장 큰 시그널과 가장 빈도가 높은 활성값을 바라봅니다 실생활에서 처럼 게으른 사람은 안전합니다 ( 느리고 빈도가 낮은 활성값들 ) 다른 뉴런들의 가중치와 상수값이 수정되는 동안 게으른 뉴런은 비난으로부터 벗어날 수가 있겠죠. 간단히 말해서 후방전파의 절차는 다음과 같은 핵심요소로 말씀드릴 수 있습니다.

Neurons blame the most active upstream neurons
- 후방전파는 에러를 각 계층을 거치며 전파하는 것으로 신경네트워크의 각 뉴런들이 오차를 수정하는 절차이다.
- 특정 뉴런의 오차는 뉴런의 가중치와 상수가 얼마나 변경되어야 하는지 어림잡을 수 있게 해주며 cost function에 영향을 미치게 된다.
- 후방전파를 할 때 가장 활발했던 뉴런이 가장 많은 수정을 하게 된다.
Trying it All Together
만약 여기까지 읽으셨다면 끈기에 대해서 박수를 보내드립니다. 처음에 뭐 때문에 그렇게 딥러닝이 특별한가 라는 질문에서 시작했고 이제 그 답을 드리려고 합니다. 제 개인적인 의견으로는 신경 네트워크는 다음과 같은 특성 때문에 특별합니다.
- 각 뉴런은 자체적인 모델로서 입력값에 대한 가중치와 상수값을 가지고 있습니다.
- 각 개별적인 모델/뉴런은 다른 수많은 뉴런들에게 입력값을 전달해줍니다. 따라서 우리는 다른 모델들을 연결시켜 하나의 거대한 모델을 만드는 셈이죠 이것은 신경 네트워크갓 너형적이지 않은 데이터를 포함하여 많은 곳에 적용할 수 있게 해줍니다.
- 서로 연결된 뉴런/모델들과 후방전파를 통해 가중치를 수정하는 작업은 가장 효율적으로 모델을 수정하는 것이며 이것이 데이터로부터 학습 한다는 프로세스 입니다.
Summary
- 딥러닝의 구성 : 입력값, 뉴런 ( 가중치, 상수 ), 뉴런/모델 들간의 연결, 결과값
- 전방전파 : 입력값과 뉴런의 가중치, 상수를 sigmoid 함수에 넣어서 하나의 활성 값을 만들고 다음 계층으로 전달한다. 결과값에 도달할 때까지 반복
- 후방전파 : ( 실제 값 - 최종 결과값 )을 에러 입력값으로 후방전파하여 각 뉴런/모델에서 자신의 가중치, 상수를 수정할 수 있게끔 한다. 이것이 ‘학습’이다.