Medium - Game Theory Concepts Within AlphaGo
in Trend
Trend 파악을 위한 Medium 기고문 포스팅 - 알파고에 탑재된 게임이론 개념; 딥마인드는 많은 혁신적인 AI 방법들에 영향을 줬습니다. 그러나 게임이론 개념이 없었다면 그렇게 효과적으로 동작하지 않았을 겁니다.
Introduction
바둑은 약 4천년전 동아시아에서 기원된 가장 오래된 보드게임으로 2명의 플레이어가 서로 겨루는 것입니다. 바둑은 일반적으로 181개의 흑돌과 180개의 백돌, 그리고 사각형의 격자무늬의 바둑판으로 진행됩니다. 바둑판은 19개의 수평, 수직선이 있어서 361개의 교차점이 있습니다. 각 플레이어는 (흑이 먼저 시작합니다) 자기 차례가 되면 격자무늬에 착수를 할 수 있으며 한번 놓여진 돌은 움직일 수 없습니다. 게임의 목적은 각자의 돌로 빈공간이 없도록 둘러싸서 영역을 차지하는 것으로 적의 돌을 영역안에 가두게 되면 바둑판에서 제거할 수 있습니다. 집이 많이 지은 플레이어가 이기게 됩니다.
딥마인드 팀은 과학자, 엔지니어, 머신러닝 전문가 등으로 구성되어 인공지능의 기술을 진화하기 위해 서로 협업하고 있습니다. 그들의 기술은 전세계로 퍼져서 공공의 이익과 과학적인 발견에 영향을 주었으며 안전과 윤리와 관련된 중요한 문제를 다루기 위해 외부사람들과 협력하기도 합니다. 그들의 결과물 중 가장 인상적인 것은 알파고 였습니다. 처음으로 컴퓨터 프로그램이 세계적인 바둑기사를 상대로 이기게 되었고 바둑계에서 가장 강력한 플레이어가 되었습니다. 알파고의 성공은 인공지능 방법에 혁신적인 영향을 주었고 딥러닝이나 convolutional 뉴럴 네트워크, 그리고 이런 개념들은 모두 게임이론의 영역입니다. 이포스트를 통해서는 딥마인드에서 알파고를 구축할 때 사용되었던 다양한 게임이론에 대해서 알려드리겠습니다.
Extensive Form Game
바둑은 완전한 정보가 주어지는 선형적인 게임입니다. 각 플레이어는 선형적으로 움직이며 같은 정보가 게임의 끝까지 영향을 미칩니다. 이런 선형적인 게임을 분석할 때 우리는 게임 트리를 통해서 게임의 확장을 언급하곤 합니다. 이런 게임의 확장은 각 플레이어의 가능한 움직임의 순서, 모든 결정 지점에서의 선택, 그리고 각 노드의 끝에있는 보상과 같은 여러가지 주요 측면을 가지고 있습니다.

(Livebook) :.figure
익스텐시브 형태를 분석하기 위해서 주로 쓰이는 일반적인 전략은 롤백/백워드 귀납법으로 문제의 끝에서부터 시간을 거꾸로 추론하는 것입니다. 새로운 형태의 게임에서는 롤백 전략을 쓸수도 있지만 바둑은 가능한 경우의 수가 250^150 ( 490,909,346,529,772,655,309,577,195,498,627,564,297,521,551,249,944,956,511,154,911,718,710,525,472,171,585,646,009,788,403,733,195,227,718,357,156,513,187,851,316,791,861,042,471,890,280,751,482,410,896,345,225,310,546,445,986,192,853,894,181,098,439,730,703,830,718,994,140,625,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 ) 이나 됩니다. 만약 사람이 게임트리의 모든 경우의 수를 분석한다면 바둑의 모든 경우의 수를 분석하기 위해서는 140억년보다 더 걸리게 됩니다. 딥마인드의 알파고 프로그램은 convolutional 뉴럴 네트워크를 강화하여 Monte Carlo 트리 검색을 활용했습니다. 몽테 카를로 트리 검색은 가능한 경우의 수에서 아주 일부만 들여다 보는 것으로 각각의 움직임에서 얼마나 많은 승과 패가 일어날 수 있는지 갯수를 세서 각 선택지의 가중치를 제시합니다. 다음은 바둑에서 일어날 수 있는 경우의 수를 시각화 한 것입니다.
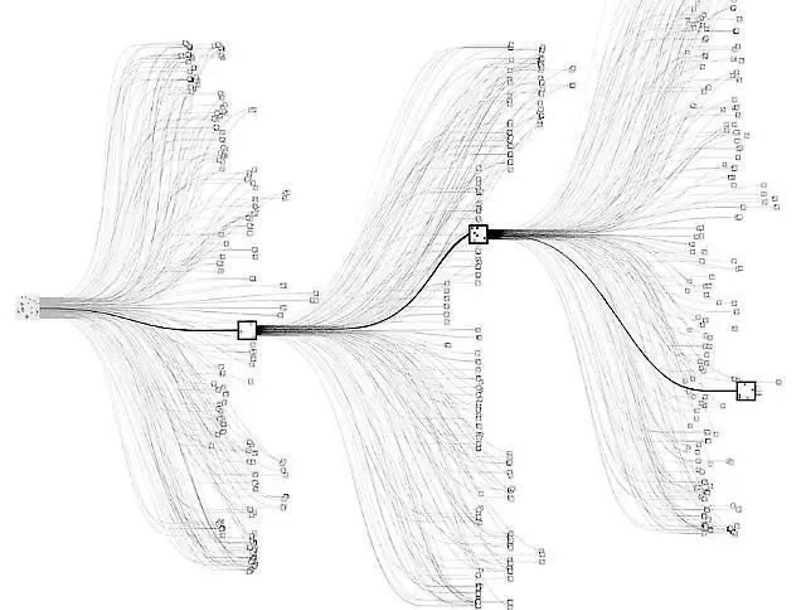
(Cheerla, 2018) :.figure
Utility Maximization
알파고가 자체적으로 가능한 움직임에 대해서 점수를 매길 때 원칙적으로 우리는 기대값을 최대로 활용하는 것을 원합니다. 강화된 뉴럴 네트워크와 몽테 카를로 트리 검색으로 알파고는 자체적으로 바둑을 두며 학습할 수 있습니다. 이런 게임에서 알파고는 가능한 움직임을 들여다보고 하나의 선택이 게임의 승률에 얼마나 영향을 주는지 예측해서 선택을 합니다. 우리는 이런 선택이 우리에게는 승률을 높여주고 적에게는 승률을 낮춰주길 원합니다. 그렇다면 가능한 경우의 수 트리를 들여다보고 어떤 선택을 하는 것이 평행적으로 승률을 높여주게 될까요?
Minimax and Alpha-Beta Pruning
미니맥스는 게임이론의 결정 규칙으로 상대 플레이어가 합리적이고 최선의 플레이를 한다고 가정한 뒤 플레이어에게 최적의 움직임을 찾는 것입니다. 양 플레이어는 차례대로 맥시마이저와 미니마이저가 되면서 각 시퀀스에서 상대방을 가장 미니마이즈 할 수 있는 움직임을 선택합니다. 적이 ( 맥시마이저 ) 여러분의 유틸리티를 미니마이징 하면서 미니맥스 알고리즘은 패배에 대한 워스트케이스 확률을 줄이는데 사용됩니다. 그러나 바둑은 경우의 수가 우주에 있는 모든 원자의 갯수보다 많기 때문에 미니맥스 알고리즘은 완전 검색을 하ㅣ가 불가능하죠. 그래서 여기서 프루닝이 사용됩니다. 프루닝은 게임트리에서 다음 단계로 넘어가지않도록 컷오프 하는 것입니다. 더욱 간단히 하자면 미니맥스 알고리즘을 계산하기 위한 경우의 수를 줄이는 것이죠. 아까 바둑의 게임트리를 확장해서 풀트리 검색을 하는데는 140억년보다 더 걸린다고 한걸 기억하시죠? 알파베타 프루닝은 몽테카를로 트리검색을 완성시켜주는 방법입니다. 몽테카를로 트리 검색 방법이 각 턴에 가능한 시퀀스의 일부만 들여다보게 되는 것이죠. 알파베타 프루닝 알고리즘이 평행하게 시행되면 아주 효과적으로 게임의 승률을 높여주는 프로그램의 의사결정을 얻을 수 있습니다.
Conclusion
딥마인드의 알파고는 최근 AI 역사에서 큰 획을 그었습니다. 딥러닝 메소드의 다양한 개발과 컴퓨터 프로세싱, 컴퓨터 하드웨어의 발전 덕분이죠. 알파고 주변에 인공지능, 머신 러닝, 강화 학습 등 많은 언어들이 떠다니지만 사실 이런 것은 모두 알파고에서 사용된 게임이론의 한 갈래입니다. 게임 이론 개념은 게임 익스텐션 폼, 백워드 귀납법, 효용 극대화 그리고 프루닝들은 거의 10년동안 있어왔으며 인공지능 응용프로그램에서 많이 활용되고 있습니다.
Summary
- 알파고가 엄청나게 많은 경우의 수를 검색하는 방법, 게임이론에서 사용되는 다양한 기법들의 조합,